黄钟第一(此章言径围之分。以十为法。凡言分者。皆十分寸之一。寸作十分。分作十釐。釐作十毫。毫作十丝。以合天地五位。终于十之数。十者全数也。体之所以立也。)
长九寸。空围九分。积八百一十分。
　算法置八百一十分。分作九重。每重九分。(法曰。置八百一十分。以九约之。)圆田术三分益一。(三分九。则分各三。益一三于九。则为十二。○法曰。置九以三分之。以四因之。)得十二。以开方法除之。得三分四釐六毫强。(强谓不尽小分也。多者为强。少者为弱。)为实径数不尽二毫八丝四忽(开方法曰。置十一分为实。借一算于二分之下。名曰廉法。乃上商三分。廉法之上。亦置三。名曰方法。方法呼商除实九分馀实三分。倍方法为六。方法一退。廉法再退。续商四釐。廉法之上。亦置四方法。共得六四呼商。除实二分五釐六毫。馀实四釐四毫。倍方法四为八。方法一退。廉法再退。续商六毫。廉法之上。亦置六方法。共得六八。六呼商。除实四釐一毫一丝六忽。不尽二毫八丝四忽。)今求圆积之数。以径三分四釐六毫。自相乘。得十一分九釐七毫一丝六忽。加以开方不尽之数二毫八丝四忽。得一十二分。以管长九十分乘之。得一千八十分。为方积之数。四分取三。(四分一千八十。则分各二百七十。去一二百七十。取三二百七十。则为八百一十。○法曰。置一千八十。以四分之以三因之。)为圆积八百一十分。
　鲁斋彭氏曰。黄钟律管。有周有径有面羃。(自上乘之曰羃

面云者。周径各自相乘。不以长乘之之义。)有空围内积。有从长。如史记论从长。律历志。论从长及积。东汉郑氏注。月令论羃。东汉蔡氏月令章句。论从长。皆不易之论。独周径之说。汉以前俱无明文。汉律历志。开端未竟。东汉蔡氏始创径三分之说。晋孟氏以后诸儒。续为径三分围九分之说。宋胡氏(安定)蔡氏(西山)又为径三分四釐六毫。围十分三釐八毫之说。然考之古方。围周径羃积。率皆未有合。(古法推之。汉蔡氏径三分自乘。得九分。三之。得二十七分。四而一。得面羃六分七釐五毫。以长九十分乘之。得内积六百一十六分五釐。晋孟氏。径三分围九分。相乘。得二十七分。四而一。亦得面羃六分七釐五毫。以长九十分乘之。亦得内积六百一十六分五釐。蔡氏，孟氏二说。羃少二分二釐五毫。积少一百九十三分五釐。宋胡氏蔡氏。径三分四釐六毫。围十分三釐八毫。相乘得三十五分九釐一毫四丝八忽。四而一。得面羃八分九釐七毫八丝七忽。以长九十分乘之。得内积八百○七分九釐八毫三丝。胡氏蔡氏二说。亦羃少二毫一丝三忽。积少二分○一毫七丝。故曰皆未有合。)尝依东汉蔡氏所言。径三分。以九章少广内祖氏密率乘除。止得空围内面羃七分○七釐奇。(密率。以径求积推之。置径三分自乘。得九分。又以一十一乘之。得九十九分一十四而一。得七分○七釐。不尽二。不尽曰奇。下皆仿此。)乃少一分九十二釐奇。空围内积实。止得六百三十六分奇。(零三法曰。置羃七分○七釐。以长九十分乘之。得六百三十六分零三。)乃少一百七十三分奇。(零八○不言三与八。而云奇者。并不尽二与八也。)如此则黄钟之

管。无乃太狭。盖黄钟空积忽微。若径内差一忽。即面羃及积所差忽数至多。此东汉蔡氏之说。所以不合也。晋孟氏诸儒言。径三分围九分。又用径一围三之法。虽是古率。然古人大约以此圆田。若以密率推之。径一则围三有奇。假如径七则围当二十有二。今依孟氏所言。径三分。则围长当九分四釐二毫八秒强。(密率。以径求周。推之。置径三分。以二十二乘之。得六十六分七而一。得九分四釐二毫八秒。不尽四。)不但止于九分也。若依九分围长之数。则径当止有二分八釐六毫三秒六忽强。(密率。以周求径。推之。置围九分七。因得六十三分二十二而一。得二分八釐六毫三秒六忽。不尽八。)又不及三分也。此晋孟氏诸儒之说。所以不合也。宋胡氏不主径三围九之说。大意疑其管狭耳。然所言径长三分四釐六毫。围长十分三釐八毫。亦用径一围三之率。(置围长三而一。)若依所言。三分四釐六毫径。当得围长十分八釐七毫四秒二忽强。(密率。以径求周。上同。)不但止于十分三釐八毫也。若依十分三釐八毫围长之数。则径止得三分三釐奇。(密率。以周求径。上同。)又不及三分四釐六毫也。此宋胡氏之说。所以不合也。宋蔡氏说径围分数。与胡氏同。至于算法。用圆田术三分益一。得一十二。开方除之求径。又以径

相乘。以管长乘之。用三分益一四分退一(四分取三而去其一分。故曰退一。馀已见算法。)之法。求羃积。今姑依其说。以九方分平置

。又三分益一。以三方分割。置于九方分之外。如

(三分九方分。则方分各三益一。三方分于九方分。则得一十二方分。外围三内方九。)共积十二方。分其纵横。可得三分四釐六毫强。不尽二毫八丝四忽。(开方法。见算法。)的如蔡氏之说。但依此径。以密率相乘。则空围内面羃。不但止得九方分。乃得九方分零四十○釐六十二毫五十七秒一十四忽奇。(密率。以径求积。推之。置径三分四釐六毫。自乘。又以一十一乘之。一十四而一。不尽四。)空围内积实。不但止得八百一十分。乃得八百四十六分五百六十三釐一百四十二秒六百忽奇。(法曰。置面羃。以长九十分乘之。)如此则黄钟之管。无乃太大。细考之。方内之圆所占者。不止四分三。(一十二方分之九方分。四分取三。而以密率。推之。面羃得九方分零四十○釐六十二毫五十七秒一十四忽。过于九分。不止四分三也。)圆外之方。所当退者又不及四分一。(一十二方分。四分退一而为九。则所当退者一。三方分而以密率推之。面羃过于九分。当退者止二分五十九釐三十七毫四十二秒八十六忽。不及三分。不及四分一也。)以此知三分益一。四分退一。乃虚加实退(三分益一。虚而加之也。四分退一。实而退之也。)算家大约之法。此宋蔡氏之说。所以又不能以尽合也。今欲求黄钟律管从长周径羃积的实定

数者。须依蔡氏多截管候气之说。又以祖氏冲之密率乘除。方可。盖祖冲之。乃古今算家之最。而蔡氏多截管候气之说。实得造律本原。其说有前人未发者。今宜依此说。先多截竹。以拟黄钟之管。或短或长长短之内。每差纤微。各为一管。悉以此诸管。埋地中。俟冬至时验之。若诸管之中。有气应者。既取其管而计之。知此管合于造化自然。非人力可为。即以此管。分作九寸。寸作九分。分作九釐。釐作九毫。毫作九秒。秒作九忽。以合八十一终天之数及元气运行。自子至亥。得十七万七千一百四十七。(置子一十一三之。)凡用此管。(用置一十一三之之数)三分损益。(三分损一阴数以两也三分益一阳数以四也)上下相生。由此。(阴损一而上生阳。阳益一而下生阴。)又取此管九寸。寸作十分。分作十釐。釐作十毫。毫作十秒。秒作十忽。以合天地五位。终于十之数。乃以十乘八十一。得八百一十分。以八百一十分。配九十分管。知此管长九十分。空围中容八百一十分。一分管长空围中。容九分。凡求度量衡由此。乃以此管面空围中所容九分。以平方羃法推之。知一分有百釐。(一分。即十釐。自乘为百釐。)釐有百毫。毫有百秒。秒有百忽。积而计之。一平方分。(方一分也。)通有面

羃一万万忽。(法曰。置十釐。自乘为百釐。又以百毫乘之。为一万毫。又以百秒乘之。为一百万秒。又以百忽乘之。为一万万忽。)九平方分。通有面羃九万万忽。(九因)乃以此九万万忽。依算经少广章所载。宋祖冲之密率乘除。得圆周长。的计十分六釐三毫六秒八忽万分忽之六千三百一十二。(密率。以积求周推之。置九万万忽。以八十八乘之。得七百九十二万万忽七而一。得一百一十三万一千四百二十八万五千七百一十四。不尽二。以一为廉法开平方除之。得一十○万六千三百六十八万六千三百一十二。不尽一○六三八六五。以万分忽之一万。约之。得十○分六釐三秒八忽万分忽之六千三百一十二奇。谓不尽数。 开方布算之法。见上算法。)又以圆周求径。计三分三釐八毫四秒四忽万分忽之五千六百四十五。(密率。以周求径推之。置圆周长十○分六釐三毫六秒八忽万分忽之六千三百一十二。通内分子得一十○万六千三百六十八万六千三百一十二。以七因之。得七十四万四千五百八十○万四千一百八十四二十二而一。得三万三千八百四十四万五千六百四十四。不尽一六。以分母一万约之。得三分三釐八毫四秒四忽万分忽之五千六百四十四奇。谓不尽数。 合不尽为五。)又以半径半周相乘。仍得九万万忽内一忽弱。(法曰。置周十○分六釐三毫六秒八忽万分忽之六千三百一十二。通分内子半之。为五万三千一百八十四万三千一百五十六。置径三分三釐八毫四秒四忽。万分忽之五千六百四十五。通分内子半之。为一万六千九百二十二万二千八百二十二。半周半径。相乘。得八万九千九百九十九万九千九百九十九万八千五百六十二零七八一。以分母一万。约之。得八万九千九百九十九万九千九百九十九忽万分忽之八千五百六十二零。七八一一忽内。少一千四百三十七零二一九。故曰一忽弱。)通得面羃九平

方分也。既以周径相乘。复得面羃。如此则黄钟之广与长及空围内积。实皆可计矣。故面羃计九方分深一分。管则空围内当有九立方分深九十分。管计九寸。则空围内当有八百一十立方分。此即黄钟一管之实。其数与天地造化。无不相合。此算法所以成也。算法既成之后。或以竹或以铜别为之。依其长各作八十一分。以为十二律。相生之法。又依其长作九十分。乃取九十分之分。计三分三釐八毫四秒四忽万分忽之五千六百四十五。以合孔径。如此则圆长面羃与夫空围内积。自然无不谐会。特径数自八毫以下。非可细分。而算法。积忽与秒不容不然。
黄钟之实第二(此章言相生之分。以九为法。凡言分者。皆九分寸之一。九丝为毫。九毫为釐。九釐为分。九分为寸。以合八十一。终天之数。九者。生数也。用之所以行也。)
子一。　黄钟之律。(三之为丑。)
丑三。　为丝法。(三之为寅。下同。)
寅九。　为寸数。
卯二十七。　为毫法。
辰八十一。　为分数。
巳二百四十三。　为釐法。

午七百二十九。　为釐数。
未二千一百八十七。　为分法。
申六千五百六十一。　为毫数。
酉一万九千六百八十三。　为寸法。
戌五万九千○四十九。　为丝数。
亥一十七万七千一百四十七。　黄钟之实。
　按黄钟九寸。以三分为损益。故黄钟之律。起于子一。三三积之。阳为黄钟寸分釐毫丝之数。阴为黄钟寸分釐毫丝之法。至于亥。而十一三之为黄钟之实一十七万七千一百四十七。还以其寸分釐毫丝之法。约之又约。得其黄钟寸分釐毫丝之数。由是损益。上下相生。律吕相间。以次长短。长者声下。短者声高。朱子曰。十七万有馀之数。以定管之长短。而出是声也。(法曰。黄钟生十一律。十一律丝毫釐分寸之数。亦以黄钟丝毫釐分寸之法约之。各得其全。以九累约。各得其寸分釐毫丝之数。)
黄钟生十一律第三(此章。言三分损益上下相生之数。其分字以上。皆黄钟之全数。即所谓法也。分字以下诸律。所取于黄钟长短之数。即所谓实也。下生者倍其实。而三其法。上生者四其实。而亦三其法。法自黄钟而三之。实亦自黄钟而倍之四之。是乃黄钟为律吕之首。而生十一律者也。)
子一分。(数起子得一。)

丑三分二。(三其法为三分。两其实为二。○法除。实乘。)
　假令置黄钟实十七万七千一百四十七。以三除之。得五万九千○四十九。以二乘之。得十一万八千○九十八。为林钟实。下同。
　一为三寸。(黄钟之寸九也。寸皆以九为数。丑三分以一为三。寸三三如九。其寸为九。寅九分一为一寸。一九如九。其寸亦九。下十辰之寸。皆黄钟之寸也。法皆仿此。)
寅九分八。(三其法。为九分。四其实。为八。)
　假令置黄钟实。法除实乘。为太簇实。(此下九辰。皆置黄钟。法除实乘。)
　一为一寸。(黄钟九寸。)
卯二十七分十六。(三法两实。)
　法除实乘。为南吕实。
　三为一寸。(黄钟九寸。)一为三分。(黄钟之分。八十一也。分皆以八十一为数。下皆仿此。)
辰八十一分。六十四。(三法四实。)
　法除实乘。为姑洗实。
　九为一寸。(九寸。)一为一分。(黄钟八十一分。)
巳二百四十三分。一百二十八。(三法两实)
　法除实乘。为应钟实。
　二十七为一寸。(九寸。)三为一分。(八十一分。)一为三釐。(黄钟之釐。

七百二十九也。釐皆以七百二十九为数。下皆仿此。)
午七百二十九分。五百一十二。(三法四实。)
　法除实乘。为蕤宾实。
　八十一为一寸。(九寸。)九为一分。(八十一分。)一为一釐。(七百二十九釐。)
未二千一百八十七分。一千○二十四。(三法两实。)
　法除实乘。为大吕实。(大吕在阳。用倍其数。)
　二百四十三为一寸。(九寸。)二十七为一分。(八十一分。)三为一釐。(黄钟七百二十九釐。)一为三毫。(黄钟之毫。六千五百六十一也。毫皆以六千五百六十一为数。下皆仿此。)
申六千五百六十一分。四千○九十六。(三法四实。)
　法除实乘。为夷则实。
　七百二十九为一寸。(九寸。)八十一为一分。(八十一分。)九为一釐。(七百二十九釐。)一为一毫。(黄钟六千五百六十一毫。)
酉一万九千六百八十三分。八千一百九十二。(三法两实。)
　法除实乘。为夹钟实。(夹钟在阳。用倍其数。)
　二千一百八十七为一寸。(九寸。)二百四十三为一分。(八十一分。)二十七为一釐。(七百二十九釐)三为一毫。(六千五百六十一毫。)一为三丝。(黄钟之丝。五万九千○四十九也。丝以五万九千○四十九为数。)
戌五万九千○四十九分。三万二千七百六十八。(三法

四实。)
　法除实乘。为无射实。
　六千五百六十一为一寸。(九寸)七百二十九为一分。(八十一分)八十一为一釐。(七百二十九釐。)九为一毫。(六千五百六十一毫。)一为一丝(黄钟五万九千四十九丝。)
亥一十七万七千一百四十七分。六万五千五百三十六。(三法两实。)
　法除实乘。为仲吕实。(仲吕在阳。用倍其数。)
　一万九千六百八十三为一寸。(九寸。○法曰。置一十七万七千一百四十七分。一万九千六百八十三而一。得九寸。馀皆仿此。)二千一百八十七为一分。(八十一分○法曰。置一十七万七千一百四十七分二千一百八十七而一。得八十一分。馀皆仿此。)二百四十三为一釐。(七百二十九釐。○法曰。置一十七万七千一百四十七分二百四十三而一。得七百二十九釐。馀皆仿此。)二十七为一毫。(六千五百六十一毫。○法曰。置一十七万七千一百四十七分二十七而一。得六千五百六十一毫。馀皆仿此。)三为一丝。(五万九千○四十九丝。○法曰。置一千七万七千一百四十七分三而一。得五万九千○四十九丝。馀皆仿此。)一为三忽。(法曰。置一十七万七千一百四十七分。以三因之。得黄钟之忽五十三万一千四百四十一忽。以九约之。得黄钟丝数。又以九约之。得黄钟毫数。又以九约之。得黄钟釐数。又以九约之。得黄钟分数。又以九约之。得黄钟寸数。此皆黄钟寸分釐毫丝之数。林钟以下十一律寸分釐毫丝之数。亦依此术求之。详见第四章。)
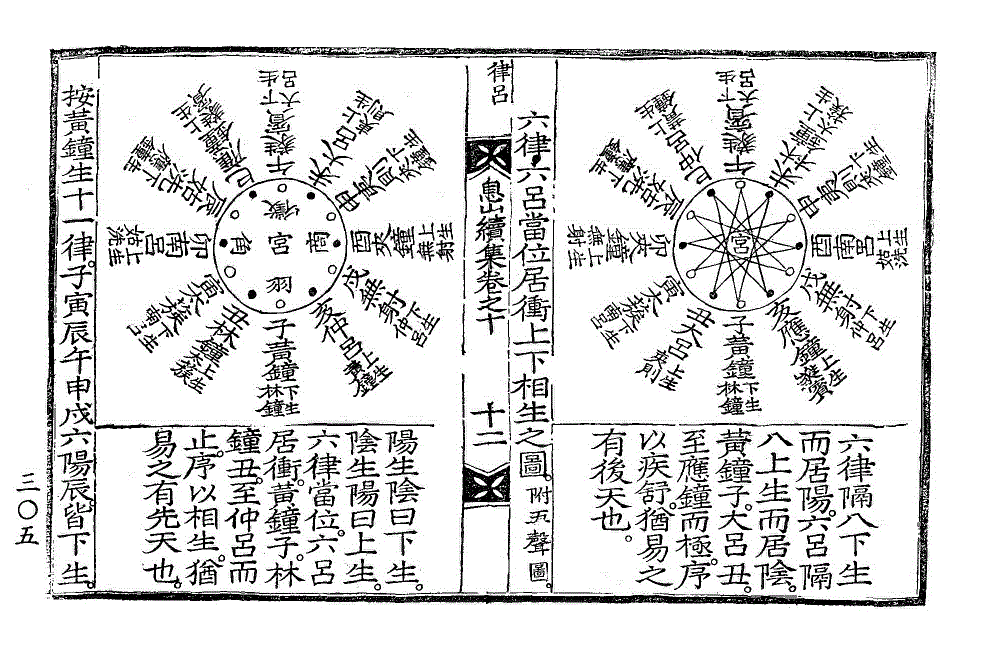
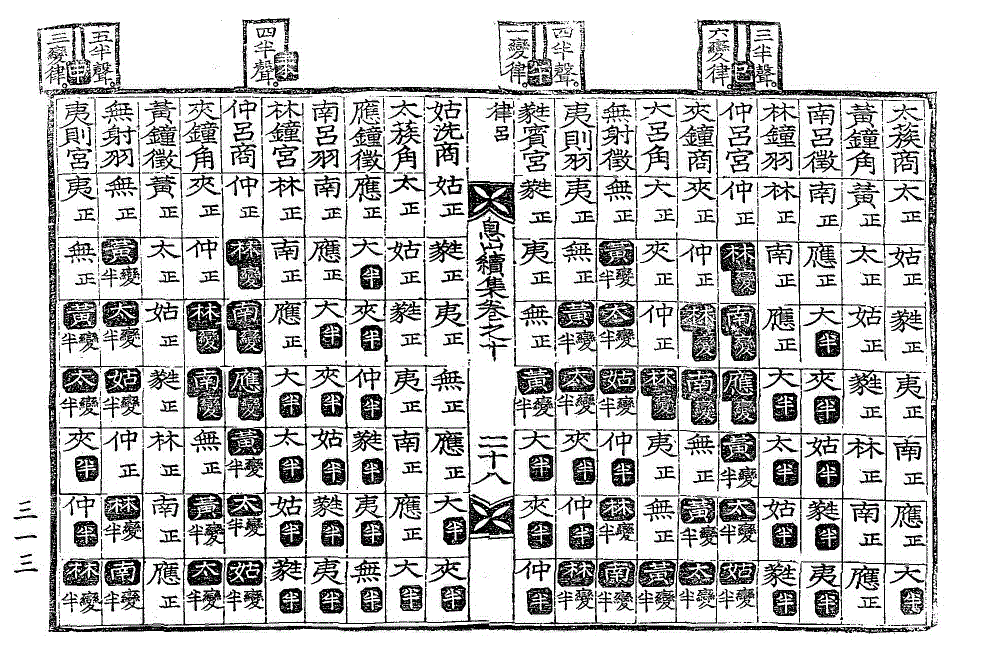
　　六律六吕上下相生之图

삽화 새창열기
　　六律，六吕当位居冲上下相生之图。(附五声图。)
삽화 새창열기
　按黄钟生十一律。子寅辰午申戌六阳辰。皆下生。

丑卯巳未酉亥六阴辰。皆上生。而淮南子，吕氏春秋，杜佑通典所论。应钟以上上下生。与大吕夹钟仲吕用倍数则虽同。而蕤宾以下以下生为上生。以上生为下生。自多数而生寡数者为下生。自寡数而生多数者为上生。牵其数之多寡。为其生之上下。盖只用大吕夹钟仲吕之倍数。而不思大吕夹钟仲吕倍前相生之数。而损益之也。如此则阴阳失序。律吕错乱。非其本法。玆敢赘图。以助参考。
十二律之实第四(此章。言十二律之实约。以寸分釐毫丝之法。得其寸分釐毫丝之全数。管之长短。于是而定。声之舒疾。由是而出也。)
子黄钟一十七万七千一百四十七。(三分损一。下生林钟。)
　假令三分黄钟实一十七万七千一百四十七。则分各五万九千○四十九。损其一。去五万九千○四十九于一十七万七千一百四十九。则得一十一万八千○九十八。为林钟之实。(法曰。置黄钟实。以三除。以二乘。下损一皆同。)
　全九寸。(法曰。置黄钟实。以寸法约之。○寸法。一万九千六百八十三。)
　半无。(黄钟君象。其正声。不为他律役。半声。亦无所用也。)
丑林钟一十一万八千○九十八。(三分益一。上生太簇。)
　假令三分林钟实一十一万八千○九十八。则分

各三万九千三百六十三。益其一。加三万九千三百六十三于一十一万八千○九十八。则得一十五万七千四百六十四。为太簇之实。(法曰。置林钟实。以三除。以四乘。下益一皆同。)
　全六寸。(法曰。置林钟实。以寸法约之。)
　半三寸。(法曰。置林钟实半之。以寸法约之。)不用(林钟在阴。无所增损。不用半声。)
寅太簇十五万七千四百六十四。(三分损一。下生南吕。)
　假令三分太簇实。损其一。为南吕之实。(三除二乘。)
　全八寸。(约以寸法。)
　半四寸。(置实半之。约以寸法。)
卯南吕十○万四千九百七十六。(三分益一。上生姑洗。)
　假令三分南吕实。益其一。为姑洗之实。(三除四乘。)
　全五寸三分。(置实。约以分法。得全分。以九约之。得寸。馀实为分。)
　半二寸六分。(置实半之。约法上同。)不用。(南吕在阴。无所增损。不用半声。)
辰姑洗十三万九千九百六十八。(三分损一。下生应钟。)
　假令三分姑洗实。损其一。为应钟之实。(三除二乘。)
　全七寸一分。(约法上同。)
　半三寸五分。(置实半之。约法上同。)
巳应钟九万三千三百一十二。(三分益一。上生蕤宾。)
　假令三分应钟实。益其一。为蕤宾之实。(三除四乘。)
　

全四寸六分六釐。(置实。约以釐法。以九累约。)
　半二寸三分三釐。(置实半之。约法上同。)不用。(应钟在阴。无所增损。不用半声。)
午蕤宾十二万四千四百一十六。(三分损一。下生大吕。)
　假令三分蕤宾实。损其一。得八万二千九百四十四。为大吕之实。大吕在阳。用倍数为十六万五千八百八十八。(三除二乘。用倍其数。)
　全六寸二分八釐。(约法上同。)
　半三寸一分四釐。(置实半之。约法上同。)
未大吕十六万五千八百八十八。(三分益一。上生夷则。)
　假令三分大吕实八万二千九百四十四。益其一。为夷则之实。(三除四乘。)
　全八寸三分七釐六毫。(约以毫法。以九累约。)
　半四寸一分八釐三毫(置实半之。约法上同。)
申夷则十一万○五百九十二。(三分损一。下生夹钟。)
　假令三分夷则实。损其一。得七万三千七百二十八。为夹钟之实。夹钟在阳。用倍数为十四万七千四百五十六。(三除二乘。用倍其数。)
　全五寸五分五釐一毫。(约法上同。)
　半二寸七分二釐五毫。(置实半之。约法上同。)
酉夹钟十四万七千四百五十六。(三分益一。上生无射。)
　

假令三分夹钟实七万三千七百二十八。益其一。为无射之实。(三除四乘。)
　全七寸四分三釐七毫三丝。(约以丝法。以九累约。)
　半三寸六分六釐三毫六丝。(置实半之。约法上同。)
戌无射九万八千三百○四。(三分损一。下生仲吕。)
　假令三分无射实。损其一。得六万五千五百三十六。为仲吕之实。仲吕在阳。用倍数为十三万一千○七十二。(三除二乘。用倍其数。)
　全四寸八分八釐四毫八丝。(约法上同。)
　半二寸四分四釐二毫四丝。(置实半之。约法上同。)
亥仲吕十三万一千○七十二。(三分不尽。)
　假令三分仲吕实六万五千五百三十六。则分各二万一千八百四十五不尽一。算至倍数十三万一千○七十二。以三分之。分各四万三千六百九十不尽二。算其数不行。此律之所以止于十二也。全六寸五分八釐三毫四丝六忽。(法曰。置仲吕实十三万一千○七十二为实。一为三忽。以三因之。得仲吕全忽三十九万三千二百一十六。以九约之。得仲吕全丝四万三千六百九十。无忽则先以丝法。三约之。 馀实为六忽。以丝九约。得仲吕全毫四千八百五十四。馀实为四丝。以毫九约。得仲吕全釐五百三十九。馀实为三毫。以釐九约。得仲吕全分五十九。馀实为八釐。以分九约。得仲吕全寸六。馀实为五分。共得六寸五分八釐四丝六忽。馀皆仿此。变律。亦同。○一法置

仲吕实十三万一千○七十二。以寸法 一万九千六百八十。 三约之。得六寸。馀实一万二千九百七十四不满。法去寸法。以分法。二千一百八十七。 约之。得五分。馀实二千○三十九不满。法去分法。以釐法。二百四十三。 约之。得八釐。馀实九十五不满。法去釐法。以毫法。二十七。 约之。得三毫。馀实一十四不满。法去毫法。以丝法三约之。得四丝。馀二。算一为三忽。得六忽。○此法虽非本法。似为简易。二术并行。不相为悖。变律以下。只以此术求之。)
　半三寸二分八釐六毫二丝三忽。(置实半之。约法上同。)
　按黄钟，太蔟，姑洗，蕤宾，夷则，无射六律。则黄钟子而子。太蔟寅而寅。姑洗辰而辰。蕤宾午而午。夷则申而申。无射戌而戌。皆阳之阳。而当位自得。林钟，南吕，应钟，大吕，夹钟，仲吕六吕。则林钟未而丑。南吕酉而卯。应钟亥而巳。阴之生始于午而穷于亥。未酉亥阴之生也。丑卯巳阴之位也。其林钟，南吕，应钟三吕。阴之阴而无所增损。只用损一之数。不用半声。大吕丑而未。夹钟卯而酉。仲吕巳而亥。阳之生始于子而极于巳。丑卯巳阳之生也。未酉亥阴之位也。其大吕夹钟仲吕三吕。阴之阳而有所增损。用其损一之数。又倍其数。亦用半声。故曰六阳辰当位。自得六阴辰。则居其冲。三吕在阴无所增损。三吕在阳则用倍数。方与十二月之气相应。盖阴之从阳自然之理也。

变律第五(此章。承上章言自黄钟至仲吕。算有不尽。数不可行。生道穷矣。遂复变而再生变律。律当变者有六。故置一而六三之。得七百二十九。以七百二十九乘。除仲吕之实。三分损益。再生黄钟，林钟，太蔟，南吕，姑洗，应钟六变律。其声近正而少高于正律。非人之所能为。乃数之自然。所以和六律之相取也。然变律非正律。故不为宫也。○法曰。置一算。一三之得三。两三之得九。三三之。得二十七。四三之。得八十一。五三之得二百四十三。六三之。得七百二十九。)주-D001
　　假令三分益一。置仲吕实十三万一千○七十二。以七百二十九乘之。为九千五百五十五万一千四百八十八。以三分之。分各三千一百八十五万○四百九十六。益其一。加三千一百八十五万○四百九十六于九千五百五十五万一千四百八十八。则得一万二千七百四十○万一千九百八十四。还以七百二十九除之。得再生黄钟实十七万四千七百六十二。(以从十二律之实下同)小分四百八十六。纪其馀分。以为忽秒。洪纤高下。不相夺伦。下同。○为法之数七百二(二十)九。实不满法。故有小分。
黄钟十七万四千七百六十二。(小分四百八十六。○三分损一。下生林钟。○三除二乘。)
　假令置黄钟再生实十七万四千七百六十二。以七百二十九乘之。得一万二千七百四十○万一

千四百九十八。加小分四百八十六。共为一万二千七百四十○万一千九百八十四。以三分之。分各四千二百四十六万七千三百二十九。损其一。去四千二百四十六万七千三百二十九于一万二千七百四十○万一千九百八十四。则得八千四百九十三万四千六百五十六。还以七百二十九除之。得再生林钟实十一万六千五百○八。小分三百二十四。下同。
　全八寸七分八釐一毫六丝二忽不用。(法曰。置黄钟变实十七万四千七百六十二。小分四百八十六。共为列实十七万四千七百六十二○四百八十六。小分百则越一位而立。十则越二位而横。 以寸法 一万九千六百八十三。 约之。得八寸。馀实一万七千二百九十八○四百八十六不满。法去寸法。以分法 二千一百八十七。 约之。得七分。馀实一千九百八十九○四百八十六不满。法去分法。以釐法 二百四十三。 约之。得八釐。馀实四十五○四百八十六不满。法去釐法。以毫法 二十七。 约之。得一毫。馀实一十八○四百八十六不满。法去毫法。以丝法三约之。得六丝。馀小分四百八十六。以忽法约之。得二忽。下同。)
　半四寸三分八釐五毫三丝一忽。(置实及小分并半之。共为列实八万七千三百八十一○二百四十三。约法。上同。)
林钟十一万六千五百○八。(小分三百二十四。○三分益一。上生太蔟。○三除四乘。)
　假令置林钟变实以七百二十九乘之。加小分三

分益一。还以七百二十九除之。得再生太蔟之实全五寸八分二釐四毫一丝一忽三初。(约法。上同。馀小分三百二十四。以忽法约之。得一忽。馀八十一。以初法约之。得三初。)
　半二寸八分五釐六毫五丝。○六初。(置实及小分并半之。约法。上同。馀小分一百六十二。以初法约之。得六初。)
太蔟十五万五千三百四十四。(小分四百三十二。○三分损一。下生南吕。○三除二乘。)
　假令置太蔟变实。以七百二十九乘之。加小分。三分损一。还以七百二十九除之。得再生南吕之实。全七寸八分。○二毫四丝四忽七初不用。(不满釐法。径用毫法。约法。上同。馀实一。得三忽。馀小分四百三十二。以忽法约之。得一忽。共得四忽。馀一百八十九。以初法约之。得七初。)
　半三寸八分四釐五毫六丝六忽八初。(置实及小分并半之。约法。上同。馀实二。得六忽。馀小分二百一十六。以初法约之。得八初。)
南吕十○万三千五百六十三(小分四十五。○三分益一。上生姑洗。○三除四乘。)
　假令置南吕变实。以七百二十九乘之。加小分。三分益一。还以七百二十九除之。得再生姑洗之实。全五寸二分三釐一毫六丝。○一初六秒。(约法上同。馀小分四十五不满。忽法以初法约之。得一初。馀一十八。以秒法约之。得六初。)
　

半二寸五分六釐○七丝四忽五初三秒。(置实及小分并半之。约之。○不满毫法。径用丝法。约法。上同。馀实一半。一为三忽。半为一忽半。共得四忽半。九初为忽。半为四初半。馀小分二十二。半除。半初法一十三半。而为半初。共得五初。馀九。以秒法约之。得三秒。)
姑洗十三万八千○八十四。(小分六十。○三分损一。下生应钟。○三除二乘。)
　假令置姑洗变实。以七百二十九乘之。加小分。三分损一。还以七百二十九除之。得再生应钟之实。全七寸○一釐二毫二丝○二初二秒不用。(约法。上同。)
　半三寸四分五釐一毫一丝。○一初一秒。(约法。上同。)
应钟九万二千○五十六。(小分四十。○三分不尽。)
　
假令置应钟变实九万二千○五十六。以七百二十九乘之。为六千七百一十○万八千八百二十四。加小分四十。共为六千七百一十○万八千八百六十四。以三分之。又不尽一算。数又不可行。此变律之所以止于六也。
　全四寸六分○七毫四丝三忽一初四秒。(约法上同。馀一算。)
　半二寸三分○三毫六丝六忽○六秒强。(约法上同。强谓不尽二算也。)不用。
　按十二律各自为宫以生五声。二变其黄钟，林钟，

太蔟，南吕，姑洗，应钟六律。则能具足。至蕤宾，大吕，夷则，夹钟，无射，仲吕六律。则取黄钟，林钟，太蔟，南吕，姑洗，应钟六律之声。少下不和。故有变律。变律者。其声近正而小高于正律也。盖黄钟正九寸。大吕正八寸三分奇。大吕取黄钟之声。其声少下。必有黄钟变八寸七分奇。则其声少高于正律。而大吕取之。高下相济。音节相和。是故变律。谓之和声。林钟以下仿此。　或问变律。少高于正律。以和其六律相取之声。则黄钟，太蔟，姑洗三变之不用。应钟变半之不用。何也。曰乐家。大率最忌臣民凌君。在十二律。则黄钟为君。在五声。则宫为君。臣民事物。莫不有序。盖若大吕为宫。黄钟为变宫时。大吕正八寸三分有馀。黄钟变八寸七分有馀。夹钟为宫。太蔟为变宫时。夹钟正七寸四分有馀。太蔟变七寸八分有馀。仲吕为宫。姑洗为变宫时。仲吕正六寸五分有馀。姑洗变七寸空有馀。黄钟，太蔟，姑洗之变。过于大吕，夹钟，仲吕之宫。便自有相凌处。其黄钟，太蔟，姑洗三变之不用。理数之自然。应钟在阴。无所增损。且诸律半声。既皆轻清。而应钟正变俱极短高。又用其半。则短之短高而高。不成声

而气不应。应钟变半之不用。亦理之自然也。朱子曰。再生之黄钟。不及九寸。只是八寸有馀。然黄钟君象也。非诸宫之所能役。故虚其正而不复用。所用只再生之变。而又缺其半。盖若大吕为宫。黄钟为变宫时。黄钟管最长。所以只得用其半。其馀宫。亦仿此。
律生五声图第六(此章言十二律旋相为宫。各生五声。黄钟之数九九八十一。是为五声之本。而为宫。三分损益。以生徵商羽角之数。以下十一律。亦各有五声。其为宫商之法。皆同。)
宫声八十一。(三分损一下生徵。)
　
假令三分宫八十一。则分各二十七。损其一。去二十七于八十一。则得五十四。为徵声之数。(三除二乘。)
徵声五十四。(三分益一。上生商。)
　假令三分徵五十四。则分各一十八。益其一。加一十八于五十四。则得七十二。为商声之数。(三除四乘。)
商声七十二。(三分损一。下生羽。)
　假令三分商七十二。则分各二十四。损其一。去二十四于七十二。则得四十八为羽声之数。(三除二乘。)
羽声四十八。(三分益一。上生角。)
　假令三分羽四十八。则分各一十六。益其一。加一

十六于四十八。则得六十四。为角声之数。(三除四乘。)
角声六十四。(三分不尽。)
　假令三分角六十四。则分各二十一。而不尽一算。数不可行。此声之所以止于五也。
　林钟以下十一律。各有五声之法。置林钟本实十一万八千○九十八。以八十一(九九黄钟之数)。乘之。得九百五十六万五千九百三十八。为宫。以本实十一万八千○九十八约之。得八十一。三分宫损一为徵。三分徵益一为商。三分商损一为羽。三分羽益一为角。宫固八十一。商亦七十二。角亦六十四。徵亦五十四。羽亦四十八矣。太蔟以下十律。皆仿此。
变声第七(此章承上章言。自宫至角。算有不尽。既不可行。当有以通之。声之变者。有二。故置一而两三之。得九。以九乘除。角声之数三分损益。再生变宫变徵二变声。变宫少高于羽。变徵少下于徵。宫羽之间。有变宫。角徵之间。有变徵。亦非人之所能为。出于理数之自然。所以济五声之不及也。然变律非正。故不为调也。)
　　假令三分损一。置角声数六十四。以九因之。为五百七十六。以三分之。分各一百九十二。损其一。去一百九十二于五百七十六。则得三百八十四。还以九约之。得再生变宫数四十二。(以从五声之数。)小分六。(纪其馀分。以为强弱。○实不满。法有小分。)

变宫四十二。(小分六。○三分益一。上生变徵。○三除四乘。)
　假令置变宫数四十二。以九因之。为三百七十二。加小分六。共为三百八十四。以三分之。分各一百二十八。益其一。加一百二十八于三百八十四。则得五百一十二。还以九约之。得再生变徵数五十六。小分八。
变徵五十六。(小分八。○三分不尽。)
　假令置变徵数五十六。以九因之。为五百○四。加小分八。共为五百一十二。以三分之。分各一百七十。而又不尽二算。其数又不行。此变声所以止于二也。
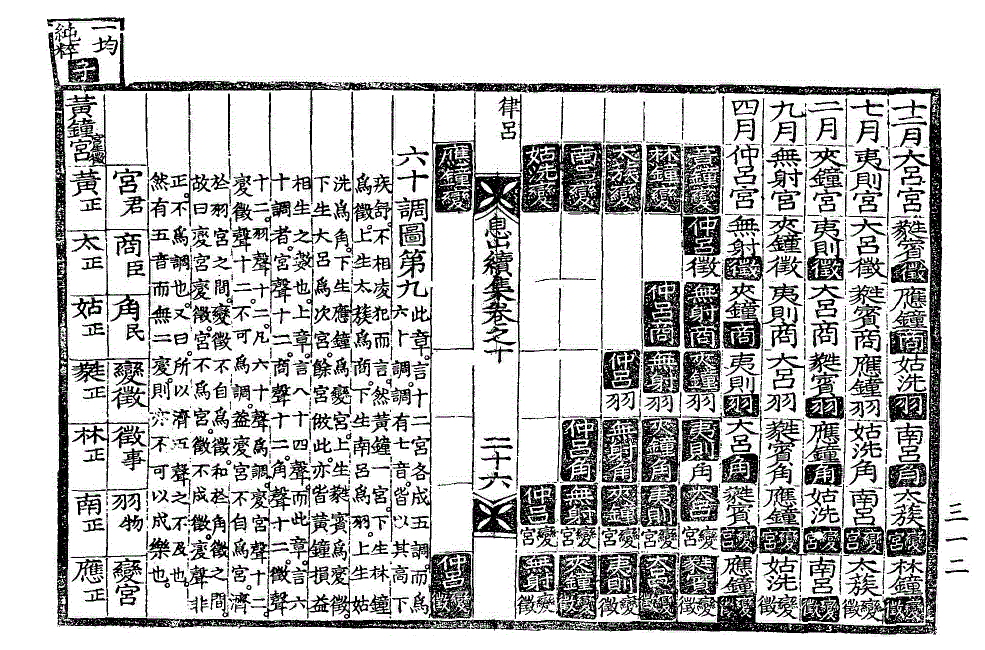
八十四声图第八(此章。言十二律旋相为宫。各有七声。而为八十四声。其十二律五声二变。皆以上下相生而言之也。○正律。墨书。半声。朱书。变律朱书。半声墨书。)
十一月黄钟宫
六月林钟宫黄钟徵
正月太蔟宫林钟徵黄钟商
八月南吕宫太蔟徵林钟商黄钟羽
三月姑洗宫南吕徵太蔟商林钟羽黄钟角
十月应钟宫姑洗徵南吕商太蔟羽林钟角黄钟变宫
五月蕤宾宫应钟徵姑洗商南吕羽太蔟角林钟变宫黄钟变徵

十二月大吕宫蕤宾徵应钟商姑洗羽南吕角太蔟变宫林钟变徵
七月夷则宫大吕徵蕤宾商应钟羽姑洗角南吕变宫太蔟变徵
二月夹钟宫夷则徵大吕商蕤宾羽应钟角姑洗变宫南吕变徵
九月无射宫夹钟徵夷则商大吕羽蕤宾角应钟变宫姑洗变徵
四月仲吕宫无射徵夹钟商夷则羽大吕角蕤宾变宫应钟变徵
黄钟变仲吕徵无射商夹钟羽夷则角大吕变宫蕤宾变徵
林钟变仲吕商无射羽夹钟角夷则变宫大吕变徵
太蔟变仲吕羽无射角夹钟变宫夷则变徵
南吕变仲吕角无射变宫夹钟变徵
姑洗变仲吕变宫无射变徵
应钟变仲吕变徵
六十调图第九(此章。言十二宫各成五调。而为六十调。调有七音。皆以其高下疾舒。不相凌犯而言。然黄钟一宫。下生林钟为徵。上生太蔟为商。下生南吕为羽。上生姑洗为角。下生应钟为变宫。上生蕤宾为变徵。下生大吕为次宫。馀宫仿此。亦皆黄钟损益相生之数也。上章。言八十四声。而此章。言六十调者。宫声十二。商声十二。角声十二。徵声十二。羽声十二。凡六十声为调。变宫声十二。变徵声十二。不可为调。盖变宫不自为宫。济于羽宫之间。变徵不自为徵。和于角徵之间。故曰变宫变徵。宫不为宫。徵不成徵。变声非正。不为调也。又曰。所以济五声之不及也。然有五音而无二变。则亦不可以成乐也。)
宫(君)商(臣)角(民)变徵徵(事)羽(物)变宫
子주-D001黄钟宫(宫生徵黄钟宫至夹钟羽。并用黄钟起调。黄钟毕曲。下皆仿此。一半声。)黄(正)太(正)姑(正)蕤(正)林(正)南(正)应(正)

(无生仲商生羽)无射商无(正四寸八分八四八)黄(变半)太(变半)姑(变半)仲 半林(变半)南(变半夷生夹角生宫)夷则角夷(正)无(正)黄(变半)太(变半)夹 半仲 半林(变半仲生黄徵生商)仲吕徵仲(正)林(变)南(变)应(变)黄(变半)太(变半)姑(变半夹生无羽生角)夹钟羽夹(正)仲(正)林(变)南(变)无(正)黄(变半)太(变半)
丑(大生夷宫生徵)大吕宫(大吕起调。大吕毕曲。)주-D004大(正)夹(正)仲(正)林(变)夷(正)无(正)黄(变半应生蕤商生羽)应钟商应(正)大 半夹 半仲 半蕤 半夷 半无 半
(南生姑角生宫)南吕角南(正)应(正)大 半夹 半姑 半蕤 半夷 半
(蕤生大徵生商)蕤宾徵蕤(正)夷(正)无(正)黄(变半)大 半夹 半仲 半
(姑生应羽生角)姑洗羽姑(正)蕤(正)夷(正)无(正)应(正)大 半夹 半
寅(太生南下皆仿此)太蔟宫(一半声)太(正)姑(正)蕤(正)夷(正)南(正)应(正)大 半
黄钟商黄(正)太(正)姑(正)蕤(正)林(正)南(正)应(正)
无射角无(正)黄(变半)太(变半)姑(变半)仲 半林(变半)南(变半)
林钟徵林(正)南(正)应(正)大 半太 半姑 半蕤 半
仲吕羽(二半声。)仲(正)林(变)南(变)应(变)黄(变半)太(变半)姑(变半)
卯夹钟宫(四变律。)夹(正)仲(正)林(变)南(变)无(正)黄(变半)太(变半)
大吕商大(正)夹(正)仲(正)林(变)夷(正)无(正)黄(变半)
应钟角应(正)大 半夹 半仲 半蕤 半夷 半无 半
夷则徵夷(正)无(正)黄(变半)太(变半)夹 半仲 半林(变半)
蕤宾羽蕤(正)夷(正)无(正)黄(变半)大 半夹 半仲 半
辰姑洗宫(二半声)姑(正)蕤(正)夷(正)无(正)应(正)大 半夹 半

太蔟商太(正)姑(正)蕤(正)夷(正)南(正)应(正)大 半
黄钟角黄(正)太(正)姑(正)蕤(正)林(正)南(正)应(正)
南吕徵南(正)应(正)大 半夹 半姑 半蕤 半夷 半
林钟羽(三半声。)林(正)南(正)应(正)大 半太 半姑 半蕤 半
巳仲吕宫(六变律。)仲(正)林(变)南(变)应(变)黄(变半)太(变半)姑(变半)
夹钟商夹(正)仲(正)林(变)南(变)无(正)黄(变半)太(变半)
大吕角大(正)夹(正)仲(正)林(变)夷(正)无(正)黄(变半)
无射徵无(正)黄(变半)太(变半)姑(变半)仲 半林(变半)南(变半)
夷则羽(四半声。)夷(正)无(正)黄(变半)太(变半)夹 半仲 半林(变半)
午蕤宾宫(一变律。)蕤(正)夷(正)无(正)黄(变半)大 半夹 半仲 半
姑洗商姑(正)蕤(正)夷(正)无(正)应(正)大 半夹 半
太蔟角太(正)姑(正)蕤(正)夷(正)南(正)应(正)大 半
应钟徵应(正)大 半夹 半仲 半蕤 半夷 半无 半
南吕羽南(正)应(正)大 半夹 半姑 半蕤 半夷 半
未林钟宫(四半声。)林(正)南(正)应(正)大 半太 半姑 半蕤 半
仲吕商仲(正)林(变)南(变)应(变)黄(变半)太(变半)姑(变半)
夹钟角夹(正)仲(正)林(变)南(变)无(正)黄(变半)太(变半)
黄钟徵黄(正)太(正)姑(正)蕤(正)林(正)南(正)应(正)
无射羽(五半声。)无(正)黄(变半)太(变半)姑(变半)仲(正)林(变半)南(变半)
申夷则宫(三变律。)夷(正)无(正)黄(变半)太(变半)夹 半仲 半林(变半)

蕤宾商蕤(正)夷(正)无(正)黄(变半)大 半夹 半仲 半
姑洗角姑(正)蕤(正)夷(正)无(正)应(正)大 半夹 半
大吕徵大(正)夹(正)仲(正)林(变)夷(正)无(正)黄(变半)
应钟羽应(正)大 半夹 半仲 半蕤 半夷 半无 半
酉南吕宫(五半声。)南(正)应(正)大 半夹 半姑 半蕤 半夷 半
林钟商林(正)南(正)应(正)大 半太 半姑 半蕤 半
仲吕角仲(正)林(变)南(变)应(变)黄(变半)太(变半)姑(变半)
太蔟徵太(正)姑(正)蕤(正)夷(正)南(正)应(正)大 半
黄钟羽(六半声。)黄(正)太(正)姑(正)蕤(正)林(正)南(正)应(正)
戌无射宫(五变律。)无(正)黄(变半)太(变半)姑(变半)仲 半林(变半)南(变半)
夷则商夷(正)无(正)黄(变半)太(变半)夹 半仲 半林(变半)
蕤宾角蕤(正)夷(正)无(正)黄(变半)大 半夹 半仲 半
夹钟徵夹(正)仲(正)林(变)南(变)无(正)黄(变半)太(变半)
大吕羽大(正)夹(正)仲(正)林(变)夷(正)无(正)黄(变半)
亥应钟宫(五半声。)应(正)大 半夹 半仲 半蕤 半夷 半无 半
南吕商南(正)应(正)大 半夹 半姑 半蕤 半夷 半
林钟角林(正)南(正)应(正)大 半太 半姑 半蕤 半
姑洗徵姑(正)蕤(正)夷(正)无(正)应(正)太 半夹 半
太蔟羽太(正)姑(正)蕤(正)夷(正)南(正)应(正)大 半
　按调声之体。宫最大而沉浊。羽最细而轻清。商之

大次宫。徵之细次羽。角居四者之中。宫为君。商为臣。角为民。徵为事。羽为物。商角徵羽不得过于宫。黄钟一均。太商姑角林徵南羽。皆以正应。他律虽当其月。而为宫商角徵羽。不得其正。或用正律正半律。或用变律变半律。盖乐家忌臣民凌君。商角徵羽有过于宫。则或正或变减其半。律伦其疾舒。亦非人之所能为。乃数之自然也。半律之法。古人言之已详。谓之子声。近时所谓清声也。如以黄钟言之。自第九宫后。夷则，夹钟，无射，仲吕四宫。则或为角或为羽。或为商或为徵。若为角则是民凌其君。为商则是臣凌其君。徵事羽物。皆可类推。故制黄钟四清声用之。不可用黄钟本律。以避凌慢。林钟以下。为商为角为徵为羽。用正用变用正半用变半。皆仿此。沈存中云。惟君臣民不可相凌。事物则不必避。○或问六十各调七音。因其相生。为之疾舒。而十二各宫五声。如黄钟为宫。无射商，夷则角，仲吕徵，夹钟羽。亦因相生。为之疾舒耶。曰莫非黄钟损益上下相生。自然之数也。盖宫下生徵。仲吕再上生黄钟。徵上生商。无射下生仲吕。商下生羽。夹钟上生无射。羽上生角。夷则下生夹钟。角再

下生变宫。大吕上生夷则。变宫上生变徵。蕤宾下生大吕。下皆仿此。律则自彼生此。声则自此生彼。并皆相生。序以疾舒也。
候气第十(此章。言候气之法。升阳之数。)
候气之法。为室三重。户闭涂衅。必周密。布缇缦室中。以木为按。每律各一按。内庳外高。(加律按上。斜埋地中。入地处卑。出地处高。与地齐端。)从其方位。加律其上。(黄子大丑之类。)以葭灰实其端。(中秋白露降。采葭莩为灰。实其管端。)覆以缇缦。按历而候之。气至则吹灰动素。(为气所动灰散。为物所动灰聚。)小动为气和。大动为君弱臣强。专政之应。不动为君严猛之应。其升降之数。在冬至则黄钟九寸。(升五分一釐三毫。)大寒则大吕八寸三分七釐六毫。(升三分七釐六毫。)雨水则太蔟八寸。(升四分五釐一毫六丝。)春分则夹钟七寸四分三釐七毫三丝。(升四分三釐七毫三丝。)谷雨则姑洗七寸一分。(升四分。○五毫四丝三忽。)小满则仲吕六寸五分八釐三毫四丝六忽。(升三分。○三毫四丝六忽。)夏至则蕤宾六寸二分八釐。(升二分八釐。)大暑则林钟六寸。(升三分三釐三毫。)处暑则夷则五寸五分五釐五毫。(升二分五釐五毫。)秋分则南吕五寸三分。(升三分。○四毫一丝。)霜降则无射四寸八分八釐四毫八丝。(升二分二釐四毫八丝。)小雪则应钟四寸六分六釐。
　

律者。阳气之动。阳声之始。必声和气应。然后可以见天地之心。然非精于历数。则气节亦未易正也。
易阳生于复。(至巳穷上反下)巳乾☰☰夬☱☰大壮☳☰泰☷☰临☷☱子复☷☳(阳之升。始于子。而阴之升于上未已。)如环无端。
阴生于姤。(至亥穷上反下)亥坤☷☷剥☶☷观☴☷否☰☷遁☰☶午姤☰☴(阴之升始于午。而阳之升于上未已。)
律吕三分损益。(律尤强吕少弱)巳仲三○三四六姑四○五四三夹三三七三太四五一六大三七六子黄五分一三自子至巳差强。升阳之数。
终不复始。(律尤弱吕差强)亥应终不始无二二四八南三○四一夷二五五林三三四午蕤二分八自午至亥渐弱。
分数多寡。虽若不齐。然其丝分毫别。各有条理。此气之所以飞灰。声之所以中律也。易者。尽天下之变。善恶阴阳。无不备也。律者。致中和之用。止于至善。故纪阳而不纪阴也。
审度第十一(此章。言度生于黄钟之长。别于分。忖于寸。蒦于尺。张于丈。信于引也。)
度者。分寸尺丈引。所以度长短也。生于黄钟之长。以子谷秬黍中者九十枚。度之一为一分。(凡黍实于管中十三黍。三分黍之一。而满一分。管长一分。空围九分。即九立方分。实十三黍。三分黍之一。 积九十分。则千有二百黍矣。法曰。置三分黍之一。通分内子。得四十。以九十分乘之。得三千六百。以分母三约之。得一千二百。 故此九十黍之数。与下章一千二百黍之数。其实一也。)十分为寸。十寸为尺。十尺为丈。十丈为引。数始于一。终于十者。天地之全数也。律未成之前。有是数而未见。律成而后。数始得以形焉。度之成。在律之后。度之数。在律之前。故律之长短围径。以度之寸分之数。而定焉。
嘉量第十二(此章。言量生于黄钟之容。跃于龠。龠者。黄钟律之实也。 合于合。登于升。聚于斗。角于斛也。)
量者。龠，合，升，斗，斛。所以量多少也。生于黄钟之容以子谷秬黍中者一千二百。实其龠。以井水准其槩。以度数审其容。(一龠积八百一十分。)合龠为合。(两龠也。积一千六百二十分。)十合为升。(二十龠也。积一万六千二百分。)十升为斗。(百合二百龠也。积一十六万二千分。)十斗为斛。(二千龠千合百升也。积一百六十二万分。○一斛容黍二百四十万粒。)

谨权衡第十三(此章。言权生于黄钟之重。殊于铢。两于两。明于斤。均于匀。大于石也。)
权衡者。铢，两，斤，匀，石。所以权轻重也。生于黄钟之重。以子谷秬黍中者一千二百。实其龠。百黍一铢。一龠十二铢。二十四铢。为一两。(两龠也。)十六两。为斤。(三十二龠三百八十四铢也。)三十斤。为匀。(九百六十龠。一万一千五百二十铢。四百八十两也。)四匀。为石。(三千八百四十龠。四万六千八十铢。一万九千二百两也。)